理解K-Means聚类
| 作者 | OpenCV-Python Tutorials |
| 编译 | Vincent |
| 来源 | OpenCV-Python Tutorials |
目标
在本章中,我们将了解K-Means聚类的概念,其工作原理等。
理论
我们将用一个常用的例子来处理这个问题。
T-shirt尺寸问题
考虑一家公司,该公司将向市场发布新型号的T恤。显然,他们将不得不制造不同尺寸的模型,以满足各种规模的人们的需求。因此,该公司会记录人们的身高和体重数据,并将其绘制到图形上,如下所示:
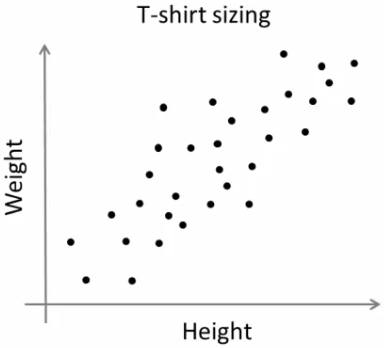
公司无法制作所有尺寸的T恤。取而代之的是,他们将人划分为小,中和大,并仅制造这三种适合所有人的模型。可以通过k均值聚类将人员分为三组,并且算法可以为我们提供最佳的3种大小,这将满足所有人员的需求。如果不是这样,公司可以将人员分为更多的组,可能是五个,依此类推。查看下面的图片:
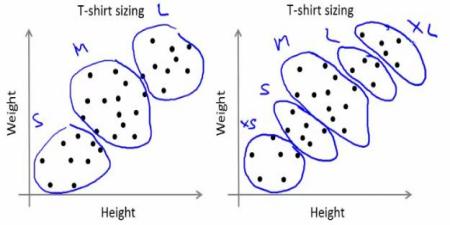
如何起作用?
该算法是一个迭代过程。我们将在图像的帮助下逐步解释它。 考虑如下一组数据(您可以将其视为T恤问题)。我们需要将此数据分为两类。
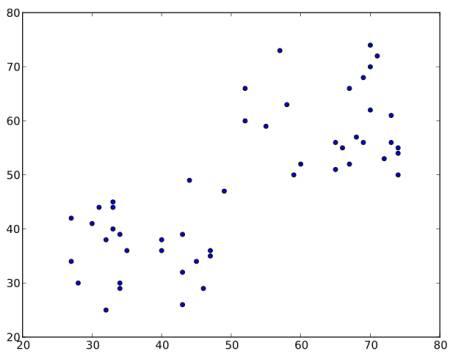
步骤:1 -算法随机选择两个质心$C_1$和$C_2$(有时,将任何两个数据作为质心)。 步骤:2 -计算每个点到两个质心的距离。如果测试数据更接近$C_1$,则该数据标记为“0”。如果它更靠近$C_2$,则标记为“1”(如果存在更多质心,则标记为“2”,“3”等)。
在我们的示例中,我们将为所有标记为红色的“0”和标记为蓝色的所有“1”上色。因此,经过以上操作,我们得到以下图像。
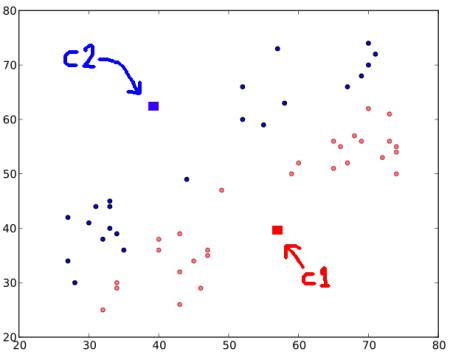
步骤:3 -接下来,我们分别计算所有蓝点和红点的平均值,这将成为我们的新质心。即$C_1$和$C_2$转移到新计算的质心。(请记住,显示的图像不是真实值,也不是真实比例,仅用于演示)。
再次,使用新的质心执行步骤2,并将标签数据设置为’0’和’1’。
所以我们得到如下结果:
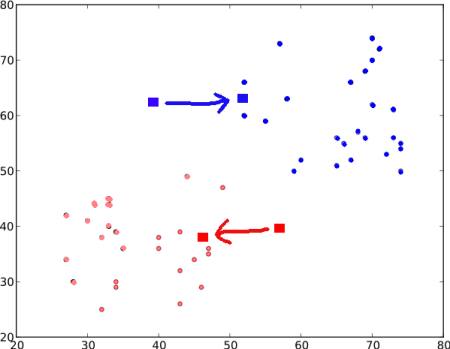
现在,迭代步骤2和步骤3,直到两个质心都收敛到固定点。(或者可以根据我们提供的标准(例如最大的迭代次数或达到特定的精度等)将其停止。)这些点使测试数据与其对应质心之间的距离之和最小。或者简单地说,$C_1↔Red_Points$和$C_2↔Blue_Points$之间的距离之和最小。
\[minimize \;\bigg[J = \sum_{All\: Red\_Points}distance(C1,Red\_Point) + \sum_{All\: Blue\_Points}distance(C2,Blue\_Point)\bigg]\]最终结果如下所示:
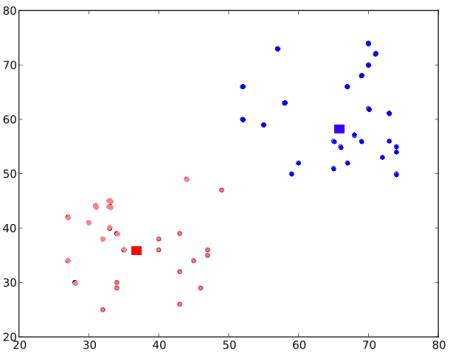
因此,这仅仅是对K-Means聚类的直观理解。有关更多详细信息和数学解释,请阅读任何标准的机器学习教科书或查看其他资源中的链接。它只是K-Means聚类的宏观层面。此算法有很多修改,例如如何选择初始质心,如何加快迭代过程等。
附加资源
- Machine Learning Course, Video lectures by Prof. Andrew Ng (Some of the images are taken from this)